Cauchy Schwarz Inequality for Integrals
Later the integral inequality. 1 Written out explicitly.

Solved The Inequality Below Is Called Cauchy Schwarz Chegg Com
Each of these terms however are still a part of the original space and hence still have a well-defined inner-product.

. Ad Browse Discover Thousands of Book Titles for Less. Cauchy Schwarz Inequality Integral. You know and love in R2 then the Cauchy-Schwartz inequality is a consequence of the law of cosines.
W w R be a continuous function that is piecewise continuously differentiable on w w. Speci cally uv jujjvjcos and cos 1. The Cauchy-Schwarz inequality also is important because it connects the notion of an inner product with the notion of length.
This means we can apply the Cauchy-Schwarz inequality. In case you are nervous about using geometric. Hot Network Questions Cannot figure out how to align these columns of equations correctly Generate an.
Looking at the proof of the Cauchy-Schwarz inequality note that 2 is. We can also derive the Cauchy-Schwarz inequality from the more general Hölders inequality. Multiplying both sides of this inequality by kvk2 and then taking square roots gives the Cauchy-Schwarz inequality 2.
Show activity on this. Cauchy-Schwarz inequality in Rn. Simply put m 2 m 2 and r 2.
If f x g x are real functions then f x g x dx 2 f x 2 dx g x 2 dx if all these integrals exist. Cauchy-Schwarz inequality for integrals in The. Need help understanding the use of Cauchy-Schwarz inequality involving.
2 with equality iff with a constant. Show activity on this post. Let and be any two real integrable functions in then Schwarzs inequality is given by.
Then we claim that the Cauchy-Schwarz Inequality holds and one can use it to deduce the triangle inequality in Rn. X ykxkkyk Triangle Inequality in Rn. That is when frac a_i b_i biai is constant for all i i.
Need help understanding the use of Cauchy-Schwarz inequality involving integrals. How to prove integral inequality using Cauchy-Schwarz. The inequality for sums was published by Augustin-Louis Cauchy while the corresponding inequality for integrals was first proved by Viktor Bunyakovsky.
Let w 0 and let f. I can prove the inequality using Riemann sums and the regular Cauchy-Schwarz inequality however I didnt see a way to prove that equality holds iff itex0int_ab f. Verfication of deduction made using the Cauchy-Schwarz inequality.

Real Analysis Question About Proof Of Showing Cauchy Schwarz Inequality Implies Schwarz Inequality From Spivak Mathematics Stack Exchange

Solved 2 The Cauchy Schwarz Inequality For Integrals Chegg Com
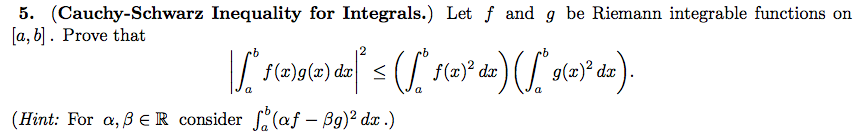
Cauchy Schwarz Inequality For Integrals Let F And Chegg Com

Real Analysis Question About Proof Of Showing Cauchy Schwarz Inequality Implies Schwarz Inequality From Spivak Mathematics Stack Exchange

Proof Of Cauchy Schwartz Inequality Mathematics Stack Exchange
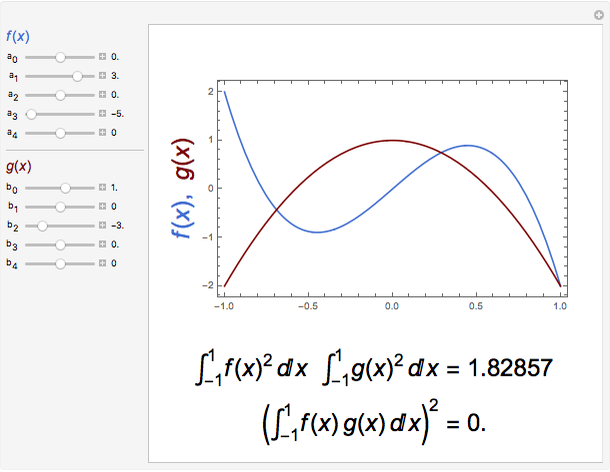
Cauchy Schwarz Inequality For Integrals Wolfram Demonstrations Project
0 Response to "Cauchy Schwarz Inequality for Integrals"
Post a Comment